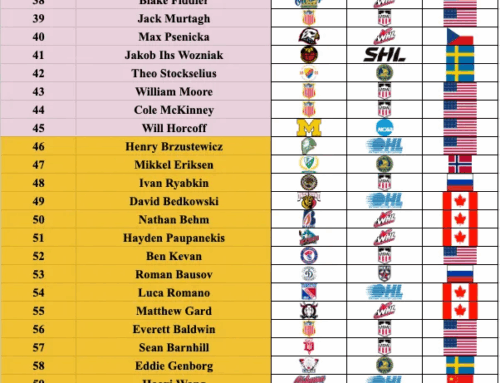
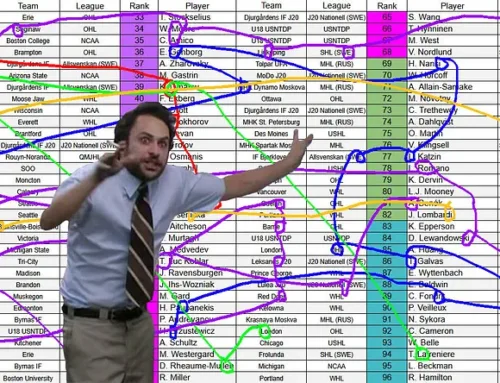
Advanced Stat Series – Value of Differing Metrics
couching
2018-01-26
The modern advent of public data and websites providing new sports metrics to evaluate players has become somewhat of a double-edged sword. On one hand, the democratization of sports statistic analysis has resulted in a whole new area of the business teams are building out, and on the other, it has polarized fans in such a gritty, historical, and noisy sport such as hockey.
The point of this column thus far has been to set the table and give background on why all metrics are tracked and how they are valued. This evolution is a trend that has occurred throughout the development of all sports, and hockey is having somewhat of a Renaissance.
This month in the column, we’ll be taking a very high-level look at the definitions and use cases of different metrics and attempt to clarify just why we track these events. But first, a quick outline of an important concept to understand beforehand.
In any statistical test, one of the most significant factors that help judge the efficacy of a study is sample size.
If sample sizes are small, variations in data will be exaggerated far heavier in analysis. To use a hockey example, if you were to try to protect the significance of the effect of shot distance and scoring goals for a certain player, and you only selected a sample size of one month of games, your potential for a weak experiment is much more likely than if you selected a sample of two months, or a season, or even a career.
Here's a look at a good supplementary article on the actual math behind variance and standard deviation here.
When it comes to hockey, the fundamental principle that analysts live by is, “if you have the puck, the other team doesn’t, therefore only you can score.” In short, having the puck = good.
Analysts quickly found that teams that take shots more, correlate heavily to teams that spend more time in the offensive zone, and the more time a team spends in an offensive zone, the more likely that team is to score more than their opponent. Of course, individual play may directly lead to goals for or against that is harder to predict, but this is where sample size comes in.
In Rob Vollman’s book, Stat Shot, he notes early on that the biggest benefit of shot attempts (or Corsi attempts, as outlined last month) is that the sample size is enormous and publically available. Over time, some analysts preferred to filter blocked shots out of the equation to isolate situations that are more likely scoring chances, commonly referred to as Fenwick attempts.
Unblocked shot attempts often come from closer to the net, and have a much higher chance of reaching higher danger areas closer to the net. Sample size is decreased, but the quality of the data appears to be slightly better. I view them as one and the same. Blocking shots may lead to less dangerous chances, but they do not negate them. Blocked shots may also add noise to the system as they are unpredictable, but they are valid data that do lead to scoring or scoring chances.
Personally, finding players who have a very high ratio of individual Fenwick attempts to individual Corsi attempts stand out to me for their ability to get pucks through defensive systems and to get more dangerous chances.
Most recently, however, metrics such as expected goals (xG) and game score (GS) have been used to increase sampled data immensely – such as quality of shooter, location of the shooter, talent of the goaltender, drawing or taking penalties, and many other metrics to boil a shot attempt into a single measure of the likelihood of a goal.
Gather enough data for an entire team and you can compare the overall quality of play and quality of scoring chances for a given game. Some have gone so far as to build prediction models for teams or even the league as a whole to varying levels of success. Many analysts relied on these models when predicting that the 2017 Nashville Predators could be a contending team.
The future appears to be studying individual playing styles and strategies that facilitate more positive possession. Plays such as controlled zone entries and exits, neutral zone transitions, and even differences between playing the body and focusing on stickwork are being looked at in various places around the league. Teams are viewing all of this through the lens of competitive advantage. If there is significant correlations between certain play styles, player types, or even basic metrics and overall goal differential, teams must be interested, no matter how small the chance of victory.
Are all these models and predictions perfect? No. Scientific work is never “perfect”.
The whole reason research is done is to try to disprove or reinforce whatever knowledge came before. It’s done to fill gaps, and to refine our knowledge and expertise. Are there off-ice factors that go into catalyzing the best possible performance out of a player or team that could work against these models? Of course that is also the case. The point is to show that in general, there are general measurements and benchmarks that correlate to a greater chance of success.
For example, if a person eats raw meat and doesn’t get sick, that doesn't mean the research showing that eating raw meat can make you sick is wrong. Analytics help identify players who may have lots left in the tank to squeeze out, such as Yanni Gourde, Jonathan Marchessault, Jason Zucker, and Mike Hoffman. They also help identify players who may have had everything squeezed out of them and may not be worth investing in like Karl Alzner, Ville Leino, Mikkel Boedker or Loui Eriksson. If you can ensure that you’re landing more players in the former category than in the latter, and you can bet that that makes your team more likely to win it all, why wouldn’t you want to investigate that phenomenon further?